| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- HTML
- aws
- 개발자취업
- Git
- 파이썬
- Azure
- 오픈소스기반데이터분석
- Python
- 데이터베이스시스템
- 프로그래머스
- JavaScript
- 클라우드컴퓨팅
- CSS
- 파이썬프로그래밍기초
- nestjs
- 꿀단집
- 방송대컴퓨터과학과
- 방송대
- 99클럽
- 코드잇
- node.js
- 항해99
- 유노코딩
- 코딩테스트준비
- redis
- 중간이들
- TiL
- mongoDB
- 코딩테스트
- 엘리스sw트랙
- Today
- Total
배꼽파지 않도록 잘 개발해요
99클럽 코테 스터디 25일차 TIL - Find if Path Exists in Graph [BFS] 본문

Find if Path Exists in Graph
출처 : LeetCode
There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n-1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
You want to determine if there is a valid path that exists from vertex source to vertex destination.
Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.
Example 1:
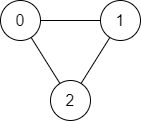
- Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
- Output: true
- Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2
Example 2:

- Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
- Output: false
- Explanation: There is no path from vertex 0 to vertex 5.
Constraints:
- 1 <= n <= 2 * 105
- 0 <= edges.length <= 2 * 105
- edges[i].length == 2
- 0 <= ui, vi <= n - 1
- ui != vi
- 0 <= source, destination <= n - 1
- There are no duplicate edges.
- There are no self edges.
틀린 풀이
/**
* @param {number} n
* @param {number[][]} edges
* @param {number} source
* @param {number} destination
* @return {boolean}
*/
var validPath = function(n, edges, source, destination) {
// 2번 예시 : [0, 1], [1, 4], [4, 5]
// 일단 시작점, 끝점 있는 배열 확인
// 정답찾기에 활용할 배열을 넣는다
// 시작점 배열의 1번 인덱스 원소로 시작하는 배열 찾는다
// 있으면 그 정답 배열에 넣고, 방금 배열의 1번 인덱스 원소로 시작하는 배열을 찾는다
// 다 찾으면(기준: 1번 인덱스 원소가 destination이랑 같음) 정답배열을 확인한다
// 길이 있는 경우 : 모든 원소가 순서대로 0, 1, 2, 5 이런식으로 이어짐.
edges = edges.sort((a, b) => a[0] - b[0]);
console.log(edges)
const arr = [edges[0]];
for (let i = 0; i < edges.length; i++) {
let [a, b] = edges[i];
for (let j = 1; j < edges.length; j++) {
let [c, d] = edges[j];
console.log("c, d", c, d)
if (b === c) {
arr.push(edges[j])
break;
}
}
}
// console.log(arr) // [ [ 0, 1 ], [ 1, 2 ], [ 2, 0 ] ]
const flatedArr = arr.flat()
const filteredArr = flatedArr.filter((el, idx) => idx === flatedArr.indexOf(el))
// console.log(filteredArr) // [ 0, 1, 2 ]
// 배열이 정렬된 상태여야 하고, 시작과 끝이 시작점과 목적지와 일치해야됨.
const con1 = filteredArr === filteredArr.sort((a, b) => a - b);
const con2 = filteredArr[0] === source
const con3 = filteredArr[n-1] === destination
console.log(con1, con2, con3)
return con1 && con2 && con3 ? true : false;
};
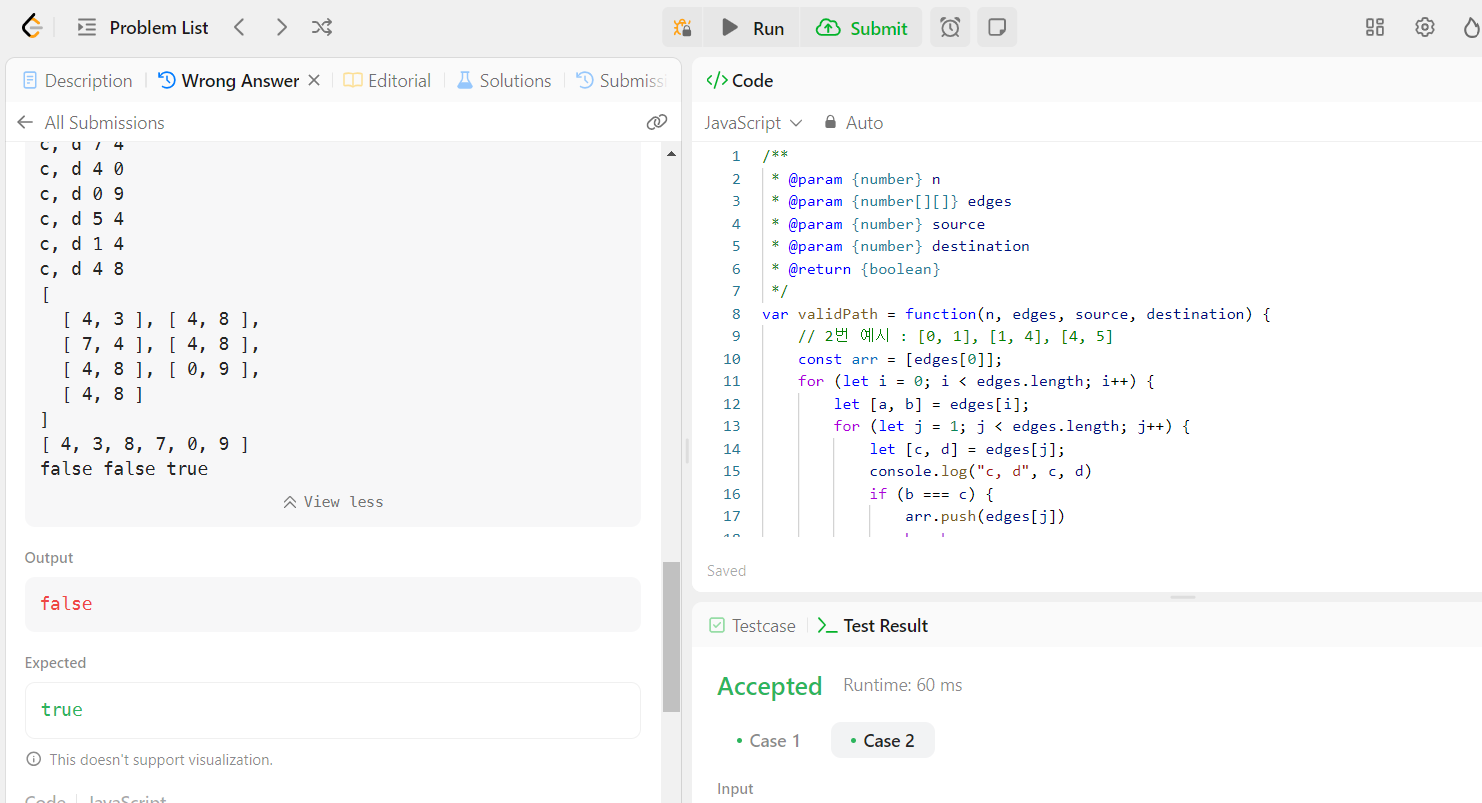
이 풀이에는 반례가 많다. 그리고 다음과 같은 치명적인 문제가 있다.
- 정렬과 필터링은 도움이 되지 않는다. 경로 찾기는 방향과 순서가 있어서 그래프의 연결성을 설명하지 못한다.
- source에서 destination까지의 경로가 있는지 순서대로 검증하지 않는다. 지금 내 풀이에서 경로의 일부분만 확인하여 true, false를 판단하고 있다.
올바른 풀이
1. 인접리스트 생성
우선 구조분해 할당으로 배열에 있는 원소를 각각 하나의 변수로 사용할 수 있도록 한다.
예를 들어 edges = [3, 4]라고 하면 인덱스0인 원소는 u, 인덱스1인 원소는 v라고 하면 된다.
그리고 초기화한 Map에는 아무것도 없을테니까 Map.set() 메서드를 이용하여 키, 값을 넣는다.
여기서 키는 u와 v이고, 값은 배열이다.
let graph = new Map();
let [u, v] = [3, 4];
if (!graph.has(u)) graph.set(u, []);
console.log("graph", graph);
// graph Map(1) { 3 => [] }
if (!graph.has(v)) graph.set(v, []);
console.log("graph", graph);
// graph Map(2) { 3 => [], 4 => [] }
대략 이런식으로 for문을 순회하면서 해당 값과 연결(인접)되어 있는 노드를 해당 키의 값인 배열에 넣어준다.
graph.get(u).push(v);
console.log("graph", graph);
// graph Map(2) { 3 => [ 4 ], 4 => [] }
graph.get(v).push(u);
console.log("graph", graph);
// graph Map(2) { 3 => [ 4 ], 4 => [ 3 ] }
이걸 코드로 작성하면 다음과 같다.
// 인접 리스트를 만들기 위한 그래프 초기화
let graph = new Map();
// 주어진 간선을 통해 그래프를 구성
for (let [u, v] of edges) {
if (!graph.has(u)) graph.set(u, []); // u가 그래프에 없으면 새롭게 초기화
if (!graph.has(v)) graph.set(v, []); // v가 그래프에 없으면 새롭게 초기화
graph.get(u).push(v); // u에서 v로 가는 간선 추가
graph.get(v).push(u); // v에서 u로 가는 간선 추가 (양방향)
}
2. BFS 초기화 (queue, set 생성)
그 다음 BFS를 시작해야하는데, 이때부터 좀 어렵다.
우선 BFS로 노드를 탐색할 때에는 큐 1개와 집합 1개가 있어야 한다.
큐는 탐색할 노드를 경로 순서대로 담는 자료구조이고, 집합은 방문했던 노드들만 모아놓는(중복 X) 자료구조이다.
source는 시작하는 노드이므로 이 큐와 집합에 각각 넣어주면 된다.
// BFS 초기화
let queue = [source]; // 탐색할 노드를 담는 큐, 시작 노드를 큐에 추가
let visited = new Set(); // 방문한 노드를 기록할 집합
visited.add(source); // 시작 노드를 방문한 노드 집합에 추가
3. BFS 진행 (queue를 순회)
이렇게 BFS를 시작할 준비가 완료되었다.
큐는 노드가 지나가는 경로이므로, 이 큐가 비어있다면 모든 탐색이 완료되었다는 의미이다. 그러므로 while문을 사용하여 큐의 길이가 0일 때 반복을 종료할 수 있도록 해준다.
while (queue.length > 0) {
// 큐의 맨 왼쪽에 있는 원소를 추출
let node = queue.shift();
// 현재 노드가 목적지라면 탐색이 완료됨.
if (node === destination) return true;
.
.
.
}
이제 반복문 쓰는 것까지 떠올렸으면 절반은 끝낸 셈이다.
큐에서 꺼낸 노드 = node
node(키), node와 인접한 노드(배열의 원소)
현재 노드와 인접한 모드를 순회한다.
만약 node = 2이고, { 2 => [3, 4, 6] } 이라면
여기서 neighbor는 순서대로 3, 4, 6이 된다.
배열이므로 for of 반복문을 쓴다.
(참고: 객체는 for in, 배열에서 for in 쓰면 인덱스값 나옴.)
for (let neighbor of graph.get(node) || []) {
// 반복문 내용
}
이웃 노드는 한번 방문했다면 1) 또다시 방문하지 않아도 되고, 방문하지 않았다면 2) 방문했다는 기록을 남겨야 한다.
따라서 이웃 노드가 처음 방문하는 곳이라면
1) 집합에 방문한 노드(neighbor)를 추가
2) 큐에 추가 (그래야 그 이웃노드 => 이웃노드의 노드 이런식으로 진행)
여기서 중요한 건, 큐는 양방향으로 입출이 가능한 자료구조이다.
현재 노드를 확인 할 때는 shift, 노드를 넣어줄 때는 push를 써야 순서가 맞다(선입선출).
// 현재 노드의 모든 이웃 노드를 탐색
for (let neighbor of graph.get(node) || []) {
if (!visited.has(neighbor)) { // 이웃 노드가 방문하지 않은 노드이면
visited.add(neighbor); // 이웃 노드를 방문한 노드 집합에 추가
queue.push(neighbor); // 이웃 노드를 큐에 추가
}
}
이런식으로 진행하다가 큐가 비어있는 상태가 되면 반복이 끝난다.
모든 이웃노드를 탐색했을 때 목적지 노드에 도달하지 않았으면 false값이 되는 것이다.
도달했다면 whlie문에서 node === destination이 true가 나온다.
참고로 이게 왜 BFS인지에 대해서 GPT가 답변을 이렇게 해줬다.
아직 BFS, DFS 등에 대해서는 잘 모르겠다.

전체 풀이
function validPath(n, edges, source, destination) {
// 인접 리스트를 만들기 위한 그래프 초기화
let graph = new Map();
// 주어진 간선을 통해 그래프를 구성
for (let [u, v] of edges) {
if (!graph.has(u)) graph.set(u, []); // u가 그래프에 없으면 새롭게 초기화
if (!graph.has(v)) graph.set(v, []); // v가 그래프에 없으면 새롭게 초기화
graph.get(u).push(v); // u에서 v로 가는 간선 추가
graph.get(v).push(u); // v에서 u로 가는 간선 추가 (양방향)
}
// BFS 초기화
let queue = [source]; // 탐색할 노드를 담는 큐, 시작 노드를 큐에 추가
let visited = new Set(); // 방문한 노드를 기록할 집합
visited.add(source); // 시작 노드를 방문한 노드 집합에 추가
// BFS 수행
while (queue.length > 0) {
let node = queue.shift(); // 큐에서 현재 노드를 꺼냄
if (node === destination) return true; // 현재 노드가 목적지 노드이면 경로가 존재하므로 true 반환
// 현재 노드의 모든 이웃 노드를 탐색
for (let neighbor of graph.get(node) || []) {
if (!visited.has(neighbor)) { // 이웃 노드가 방문하지 않은 노드이면
visited.add(neighbor); // 이웃 노드를 방문한 노드 집합에 추가
queue.push(neighbor); // 이웃 노드를 큐에 추가
}
}
}
return false; // 큐가 비어도 목적지 노드에 도달하지 못했으면 경로가 없으므로 false 반환
}
느낀점
- Map과 Set을 숙달하고 리트코드 문제를 풀며 그래프 문제 해결 능력을 길러야 할 것 같다.
- 특히 시각화 자료를 활용하여 그래프 개념을 정리하면 큰 도움이 될 듯 싶다. 나중에 프로젝트 끝나고 정리해야겠다.
'코딩테스트 > 99클럽' 카테고리의 다른 글
| 99클럽 코테 스터디 27일차 TIL - 공원 산책 (0) | 2024.08.17 |
|---|---|
| 99클럽 코테 스터디 26일차 TIL - 바탕화면 정리 (0) | 2024.08.17 |
| 광복절 맞이 아스키 아트(ASCII Art) 그리기 - 태극기 들고 있는 루피 (0) | 2024.08.15 |
| 99클럽 코테 스터디 24일차 TIL - Find Center of Star Graph (0) | 2024.08.15 |
| 99클럽 코테 스터디 23일차 TIL - Array Partition (0) | 2024.08.14 |